Inegalitatea mediilor: media aritmetică este mai mare decât media geometrică

Folosindu-ne de cea mai importantă inegalitate din gimnaziu, despre care am discutat în articolul precedent, putem obține o nouă inegalitate importantă, valabilă pentru medii.

Mai exact, dacă pornim de la două numere reale pozitive $0\leq a\leq b$, putem calcula media lor aritmetică dată de $$M_a(a,b)=\frac{a+b}{2}$$ și media lor geometrică $$M_g=\sqrt{a\cdot b}.$$

De exemplu, dacă numerele sunt $a=4$ și $b=9$, atunci media lor aritmetică este $$M_a=\frac{4+9}{2}=\frac{13}{2}=6,5$$ și $$M_g=\sqrt{4\cdot 9}=\sqrt{36}=6.$$

Observați deja că $6,5>6$ și astfel media aritmetică a celor două numere alese este mai mare decât media lor geometrică. 

Această inegalitate este una generală, în sensul că media aritmetică a două (sau mai multor) numere reale pozitive este întotdeauna mai mare sau cel puțin egală cu media lor geometrică. Deci, întotdeauna avem $$\color{red}{\frac{a+b}{2}\geq\sqrt{a\cdot b}}.$$

Căci, pornind de la cea mai importantă inegalitate din gimnaziu, care ne spune că orice număr real ridicat la puterea a doua este mai mare decât zero sau cel puțin egal cu zero, rezultă că acest lucru este valabil și pentru diferența a două numere reale pozitive, oricare ar fi ele $(x-y)^2$, adică avem $$(x-y)^2\geq 0.$$ 

Mai departe, ridicând la puterea a doua paranteza prin înmulțirea parantezei cu ea însăși sau prin utilizarea formulei de calcul prescurtat, vom avea că $$(x-y)^2=(x-y)\cdot(x-y)=x^2-xy-yx+y^2=x^2-2xy+y^2.$$ Și cum $(x-y)^2\geq 0$, rezultă că $$x^2-2xy+y^2\geq 0,$$ ceea ce mai înseamnă și $$x^2+y^2\geq 2xy$$ (am aruncat în dreapta termenul $2xy$) și mai înseamnă și $$\frac{x^2+y^2}{2}\geq xy$$ (am împărțit inegalitatea precedentă cu 2).

Acum, notând $x^2=a$ și $y^2=b$, cum $a$ și $b$ sunt pozitive, va rezulta că $x=\sqrt{a}$, $y=\sqrt{b}$ și $xy=\sqrt{a}\cdot\sqrt{b}=\sqrt{ab}$, ceea ce ne duce direct la inegalitatea mediilor.

Și există o medie (media pătratică) care este chiar mai mare decât media aritmetică. Pentru numerele concrete alese mai sus avem $$M_p=\sqrt{\frac{4^2+9^2}{2}}=\sqrt{48,5}\approx 6,96.$$

Și există o medie (media armonică) care este mai mică decât media geometrică. Media armonică a lui 4 și 9 este $$M_h=\frac{2}{\frac{1}{4}+\frac{1}{9}}=\frac{2}{0,25+0,(1)}\approx 5,53.$$

Astfel, putem sintetiza inegalitatea mediilor mai frumos: $$\color{red}{b\geq\sqrt{\frac{a^2+b^2}{2}}\geq\frac{a+b}{2}\geq\sqrt{ab}\geq\frac{2}{\frac{1}{a}+\frac{1}{b}}\geq a}.$$

Din această inegalitate celebră mai rezultă că dacă oricare două dintre aceste medii sunt egale, va rezulta că și numerele ale căror medii se calculează sunt egale, concluzie foarte subtilă ce este valorificată în unele probleme mai dificile.

Cea mai importantă inegalitate din gimnaziu!

Elevii de clasa a șasea învață să lucreze cu numere negative, mai mici decât zero. Ca exemplu, primesc temperatura mediului înconjurător sau etajele de la subsolul unor clădiri înalte. 

Li se spune că iarna, atunci când este mai frig decât frigul la care îngheață apele curate, temperatura este negativă, mercurul termometrului fiind foarte înghesuit, ocupând volum mai mic, în timp ce vara temperatura este, de regulă, pozitivă, iar mercurul termometrului este extins mai mult, dilatat mai mult. 

De exemplu, atunci când temperatura este de $-3^o$, este mai frig (nivelul mercurului este mai coborât) decât atunci când temperatura este de $+5^o$, iar diferența de temperatură în acest caz este de $8^o$, adică mercurul urcă 8 etaje ca să ajungă de la etajul $-3$ la etajul 5.

Apoi, după ce au învățat numerele negative, învață să lucreze cu puterile acestora și află că dacă exponentul la care se ridică un număr negativ este par, atunci rezultatul ridicării este un număr pozitiv. De exemplu, $(-3)^2=(-3)\cdot(-3)=+9$.

Din acest moment li se poate povesti despre cea mai importantă inegalitate din gimnaziu și anume despre faptul că $$\color{red}{orice^2\geq 0}.$$

Așadar, orice număr învățat în gimnaziu, ridicat la puterea a doua va da un rezultat pozitiv, indiferent de număr. 

În liceu se învață și alt tip de numere (așa-numitele numere complexe), care ridicate la pătrat ne pot da și un rezultat negativ.

Această inegalitate de care v-am vorbit este cea mai importantă, deoarece din ea rezultă o mulțime de alte inegalități. De exemplu, inegalitatea mediilor se demonstrează ușor cu această inegalitate importantă, ceea ce denotă că inegalitatea mediilor este o consecință frumoasă a celei mai importante inegalități din gimnaziu. 

Așadar, dragii mei, rogu-vă să vă amintiți des despre această minunăție învățată în gimnaziu, căci ea vă va scoate din belele în majoritatea cazurilor când vi se va cere să demonstrați o inegalitate.

Despre un generator automat de teste-fulger, în format pdf

Introducere

Am bucuria să anunț apariția primei versiuni (versiunea beta.5) a unui produs românesc foarte interesant și foarte util pentru o mare categorie de clienți, fie că aceștia sunt elevi, profesori sau părinți. Acest proiect, de mare anvergură, a apărut din dorința de a ajuta cât mai multă lume să înțeleagă fără profesor minunata Matematică, precum și să evalueze cunoștințele dobândite din acest domeniu. El va putea inspira și alți profesori, de la alte materii, să conceapă și ei asemenea baze de date din care calculatorul să genereze aleatoriu o mulțime de teste.

Deocamdată a apărut versiunea corespunzătoare clasei a cincea (motiv pentru care versiunea se numește „beta.5”), urmând ca în lunile și anii care vin, în limita timpului disponibil, să construiesc cu migală și pasiune celelalte baze de date până la clasa a douăsprezecea inclusiv.

Descriere

Testele-fulger sunt concepute pentru a verifica rapid cunoștințele fundamentale ale elevilor și a le confrunta cu rezolvările corecte amplasate în partea a doua a fișierului de test.

Ele caută să evite posibilitatea copierii de la colegi sau de pe internet a răspunsurilor, prin limitarea drastică a timpului de rezolvare, corelat cu limitarea dificultății problemelor.

 

Distractorii sunt concepuți cu multă migală, pe principiul ca elevul care știe să poată alege repede răspunsul corect, iar elevul care nu știe să fie, eventual, indus în eroare de unii distractori.

La cerere, testele pot fi diversificate după mai multe criterii, precum clasa, unitatea de învățare și chiar tipul itemilor. Mai precis, pot fi generate teste de clasa a cincea cu probleme dintr-o singură unitate de învățare sau mai multe. De asemenea, pot fi generate teste ale căror probleme să prezinte distractorii (itemi obiectivi cu alegere multiplă) sau să nu prezinte distractorii (itemi semiobiectivi, de completare). Pot fi generate chiar și teste care combină itemi cu distractori și itemi fără distractori.

Pot fi generate cărți întregi cu sute de astfel de teste de tipul ales inițial de către client.

Fiecare problemă generată automat de către calculator are asociat un punctaj, care împreună cu punctajul din oficiu ar trebui să totalizeze 1000 de puncte în cazul unei rezolvări complete și corecte.

Structură

Testul-fulger are un antet în care poate apărea unitatea de învățământ și numele profesorului, precum și momentul generării testului.

Apoi urmează enunțul problemelor din primul test,

care pot fi probleme fără distractori sau probleme cu distractori, după cum apare în cerința clientului:

unitățile de învățare fiind cele din structura programei pentru clasa a cincea:

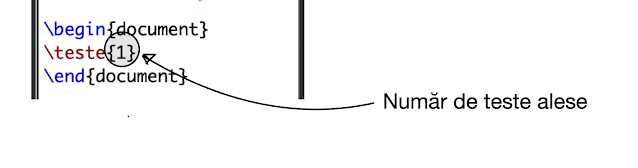
iar numărul de teste putând fi, de asemenea, modificat după dorință în interiorul fișierului-sursă LaTeX:

Testul mai conține, așa cum am considerat firesc, rezolvările și explicațiile, care apar pe o pagină nouă ca să poată fi imprimate separat și să nu le vadă la început elevul:

Pentru părinți

Părintele poate imprima unul sau mai multe dintre testele alese, împreună cu rezolvările, iar copilul va primi doar partea cu enunțuri pentru a rezolva problemele, urmând ca după rezolvarea testului, să fie confruntată rezolvarea elevului cu rezolvarea propusă prin test. Asemenea teste pot ajuta părinții nu doar să-și evalueze singuri copiii, ci chiar și să le explice rezolvarea.

Pentru profesori

Testele propuse pot ajuta enorm profesorii pentru a le da elevilor teme sau pentru a-i evalua la clasă. În funcție de nivelul clasei, profesorul poate mări (dubla, tripla) sau micșora timpul propus pentru rezolvarea testului.

Foarte important, antetul și filigranul pot fi modificate la cerere pentru profesori, folosindu-se școala și numele profesorului respectiv.

Versiuni

Versiunea de lansare este „beta.5”, însemnând că este vorba despre versiunea beta aferentă clasei a cincea, care garantează existența unui număr suficient de probleme în baza de date aferente clasei a cincea.

Următoarele versiuni vor rămâne versiuni beta până la atingerea a cel puțin 100 de probleme în fiecare unitate de învățare, caz în care versiunile vor deveni 1.5, 1.6 și așa mai departe. Așadar, primul număr al versiunii va reprezenta numărul de sute de probleme din bazele aferente unităților de învățare, iar numărul al doilea, de după punct, reprezintă clasa la care s-a ajuns cu versiunea respectivă în ordinea crescătoare a lor (începând cu clasa a cincea și terminând cu clasa a douăsprezecea).

Astfel, după versiunea beta.5 va urma versiunea beta.6, apoi beta.7 și tot așa până la apariția versiunii beta.12, după care va apărea versiunea 1.5 (cu peste 100 de probleme la fiecare unitate de învățare din clasa a cincea), apoi 1.6 (cu peste 100 de probleme la fiecare unitate de învățare din clasa a șasea) și așa mai departe.

Prețul

Prețul de pornire al acestor teste este stabilit la 10 bani pe problemă, elevii mei beneficiind de gratuitate în cursul întregului an în care le sunt mentor. Astfel, un test care va conține, de exemplu, 15 probleme va costa 1,5 lei.

Dacă clientul dorește 10 teste cu 15 probleme fiecare, se vor însuma 150 de probleme, prețul total devenind astfel 15 lei. Acest preț, împreună cu descrierea testului vor apărea automat la finalul fiecărui fișier pdf generat.

În foaia de calcul „Lungimea bazelor de date” puteți afla câte probleme am reușit să creez în fiecare dintre bazele de date până în prezent, adică găsiți ceva de genul:

V-M+F=2

Acest domn Euler a fost o minune, un înger pe Pământ. Dânsul ne-a lăsat această relație superbă, $$\color{red}{V-M+F=2}$$ care ne face legătura între numărul de Vârfuri, de Muchii și de Fețe ale unui poliedru.

Puteți reține ușor relația domnului Euler, căci literele care apar sunt în ordine alfabetică descrescătoare și avem un semn minus în mijloc.

De exemplu, o piramidă patrulateră are 

$V=4+1=5$, cinci vârfuri, $M=2\cdot 4=8$, opt muchii și $F=4+1=5$, cinci fețe. Deci, $V-M+F=5-8+5=\color{red}{2}$.

Mai vedeți și voi alte exemple, poate vă iese tot $\color{red}{2}$.