Cele zece teste recente pentru final de clasa a cincea și început de clasa a șasea

Iată câteva teste generate la începutul acestei luni:

Test-fulger, Septembrie 2024 by abelcavasi

Teorema lui Pitagora și factorul comun

Din experiența mea, peste 90% dintre elevi nu știu să folosească trucul de care vă voi vorbi în acest articol.

Este vorba despre modul rapid în care putem găsi a treia latură a unui triunghi dreptunghic atunci când le cunoaștem pe celelalte două. Desigur, se aplică teorema lui Pitagora, dar maniera de calcul este mult mai eficientă cu ajutorul factorului comun.

Așadar, să presupunem pentru început că ni se dă un triunghi dreptunghic a cărui ipotenuză are lungimea de 75 cm, iar una dintre catete are lungimea de 60 cm și se dorește determinarea celeilalte catete. 

În acest caz, un elev gospodar se va pune pe treabă utilizând teorema lui Pitagora și va scrie că 

$$c_1=\sqrt{ip^2-c_2^2}=\sqrt{75^2-60^2}=\sqrt{5625-3600}=\sqrt{2025}=45.$$

Desigur, toate au mers brici, în ipoteza că știm să ridicăm repede la pătrat numărul 75 și știm să extragem repede radical din 2025. 

Apropo! Știți să ridicați repede la pătrat un număr care se termină cu 5? E foarte fain: se înmulțește numărul din fața lui 5 cu succesorul său și se adaugă la final numărul 25, așa cum vedeți în exemplele din imaginea de mai jos.

Dar să revenim la teorema lui Pitagora. În cazul precedent (și în toate cazurile similare, cu factor comun) putem să observăm că cele două numere date în ipoteză, adică 75 și 60, au un divizor comun destul de mare, pe 15. Această observație ne va permite să facem calculele mult mai ușor. Pentru că dacă două dintre laturi au un divizor comun (desigur, ne referim la lungimile lor, prin abuz de limbaj), atunci cu certitudine și cea de-a treia latură va avea același divizor. Astfel, în cazul exemplului nostru, dacă 75 și 60 îl au ca divizor pe 15, atunci cu siguranță și 45 îl va avea ca divizor pe 15. 

Acest avantaj ne ajută să lucrăm cu numere mult mai mici. Căci, abstracție făcând de divizorul 15, triunghiul nostru se comportă acum ca și cum ar avea laturile mai mici de 15 ori. Adică, este suficient să găsim cu teorema lui Pitagora cateta necunoscută pentru un triunghi mai mic, cu laturile fără 15, după care să înmulțim înapoi cu 15.

Demonstrația acestui fapt pentru triunghiul inițial este simplă, căci putem scrie:

$$c_1=\sqrt{75^2-60^2}=\sqrt{(5\cdot\color{red}{15})^2-(4\cdot\color{red}{15})^2}=\sqrt{5^2-4^2}\cdot\color{red}{15}.$$

Cazul prezentat este mai simplu, căci se bazează pe celebrul și binecunoscutul triplet pitagoreic fundamental $\color{red}{3,4,5}$ cu derivatele sale obținute prin înmulțirea cu un factor natural. Dar utilitatea metodei descrise iese mai bine în evidență în cazuri mai complicate, cum este cazul triunghiului ale cărui catete sunt, de exemplu, 16 și 24. Cât va fi în acest caz ipotenuza?

Dacă nu aplicăm trucul, trecem prin următorul chin:

$$ip=\sqrt{16^2+24^2}=\sqrt{256+576}=\sqrt{832}.$$

Și, desigur, pentru a găsi cât este radicalul lui 832 vă veți mai chinui să-l descompuneți:

obținând, în sfârșit, ipotenuza ca fiind egală cu $8\sqrt{13}$.

Dar ce am fi câștigat dacă foloseam trucul cu factorul comun? Păi, în loc să lucrăm cu triunghiul mare, am fi descoperit că 16 și 24 îl au pe 8 ca factor comun:

și atunci lucram cu triunghiul mic

pentru a-l descoperi pe $\sqrt{13}$, adică procedam ca în imaginea:

Eu sper din toată inima ca acest truc să vă ajute să câștigați timp de-acum încolo atunci când doriți să găsiți mai rapid cea de-a treia latură a unui triunghi dreptunghic, dacă celelalte două au un divizor comun mare.

Metoda cireșelor

Acum, fiind în vacanță și înfulecând cu nesaț niște cireșe dulci și grase, am găsit ceva timp ca să vă vorbesc despre metoda de descompunere în factori a unui trinom cu coeficienți întregi, pe care în gimnaziu o numim „metoda cireșelor”, căci amintește de perechile de cireșe savuroase atârnate după urechi. 

Metoda se aplică cu mult succes la descompunerea trinomului cu coeficienți întregi pentru care coeficientul dominant (adică „a”-ul, deci coeficientul lui $x^2$) este egal cu unitatea, adică la trinoame de forma $x^2+bx+c$, unde $b$ și $c$ sunt numere întregi.

Fundamentul care stă la baza metodei cireșelor este dat de formulele lui Viète, care fac o legătură superbă între coeficienți și rădăcini.

Astfel, cu metoda cireșelor putem realiza, de exemplu, descompunerile următoare: 

(ambele numere pozitive)

$$x^2+\underset{\underset{{\color{red}{2}}+{\color{blue}{3}}}{\wedge}}{5}x+\underset{\underset{{\color{red}{2}}\cdot{\color{blue}{3}}}{\wedge}}{6}=(x+{\color{red}{2}})\cdot(x+{\color{blue}{3}}),$$

(ambele numere pozitive)

$$x^2+\underset{\underset{{\color{red}{1}}+{\color{blue}{5}}}{\wedge}}{6}x+\underset{\underset{{\color{red}{1}}\cdot{\color{blue}{5}}}{\wedge}}{5}=(x+{\color{red}{1}})\cdot(x+{\color{blue}{5}}),$$

(ambele numere negative, termenul liber rămâne pozitiv)

$$x^2\underset{\underset{({\color{red}{-2}})+({\color{blue}{-3}})}{\wedge}}{-5x}\underset{\underset{({\color{red}{-2}})\cdot({\color{blue}{-3}})}{\wedge}}{+6}=(x{\color{red}{-2}})\cdot(x{\color{blue}{-3}}),$$

(numere de semn contrar, termenul liber devine negativ)

$$x^2\underset{\underset{({\color{red}{-2}})+({\color{blue}{+3}})}{\wedge}}{+x}\underset{\underset{({\color{red}{-2}})\cdot({\color{blue}{+3}})}{\wedge}}{-6}=(x{\color{red}{-2}})\cdot(x{\color{blue}{+3}}),$$

(numere de semn contrar, termenul liber este, de asemenea, negativ)

$$x^2\underset{\underset{({\color{red}{-1}})+({\color{blue}{+5}})}{\wedge}}{+4x}\underset{\underset{({\color{red}{-1}})\cdot({\color{blue}{+5}})}{\wedge}}{-5}=(x{\color{red}{-1}})\cdot(x{\color{blue}{+5}}),$$

unde puteți observa că termenul liber se scrie ca un produs de două numere, iar coeficientul lui $x$ se scrie ca o sumă de aceleași două numere.

În fine, există desigur o metodă generală pentru a descompune orice trinom într-un produs de factori, dacă elevul știe deja să calculeze „cu delta” cele două rădăcini ale unui trinom. Prin această metodă, descompunerea trinomului general este dată de:

$$\color{red}{ax^2+bx+c=a(x-x_1)(x-x_2)},$$ unde $x_1$ și $x_2$ sunt cele două rădăcini ale trinomului.

Teorema lui Pitagora în patrulaterul ortodiagonal

Un patrulater ale cărui diagonale sunt perpendiculare se numește patrulater ortodiagonal.

Într-un patrulater ortodiagonal este valabilă o teoremă extinsă a lui Pitagora care ne spune că suma pătratelor laturilor opuse dintr-o pereche este egală cu suma pătratelor laturilor opuse din cealaltă pereche. 

Cu literele noastre, teorema lui Pitagora în patrulaterul ortodiagonal ABCD spune că:

$$AB^2+CD^2=AD^2+BC^2$$

Mai mult, dacă ne interesează aria acestui patrulater, putem observa că aceasta este dată suma ariilor celor patru triunghiuri dreptunghice care formează patrulaterul. Din acest motiv, aria patrulaterului ortodiagonal este semiprodusul lungimilor diagonalelor sale, adică

$$A_{ABCD}=\frac{AC\cdot BD}{2}.$$

Rombul și pătratul sunt, prin excelență, patrulatere ortodiagonale, deci și pentru ele sunt valabile relațiile de mai sus.

O prietenie dintre cerc și triunghiul dreptunghic, care durează de milioane de ani

Se spune că, demult, încă din negura vremurilor, cu mult înainte de apariția dinozaurilor, cercul și-a dat întâlnire cu triunghiul dreptunghic, în taină și nu s-au mai despărțit de atunci niciodată. Și nici nu se vor mai despărți vreodată, deoarece au jurat într-o prietenie veșnică. Iar ei se țin de cuvânt...

De-a lungul anilor, însă, odată cu apariția pe Pământ a omului pasionat de Matematică (homo mathematicus), taina celor două figuri geometrice a început să se risipească, în ciuda faptului că ele au rămas, totuși, prietene.

Și iată care este taina lor, ascunsă în imaginea de mai jos:

Ce trebuie să observați aici? Că unghiul CAB subîntinde semicercul roșu, adică are $90^o$, astfel că triunghiul ABC este dreptunghic în A, iar ipotenuza triunghiului dreptunghic este tocmai diametrul cercului circumscris triunghiului. 

Mai observați de aici că segmentele OA, OB și OC sunt tocmai raze ale cercului circumscris, deci sunt egale între ele, proprietate ce poartă numele de teorema medianei (mediana principală AO este jumătate din ipotenuză).

Multe probleme din geometria plană își găsesc rezolvarea în această legătură minunată de care uită majoritatea elevilor de gimnaziu. Așa că, intervenția mea are menirea de a sublinia încă o dată prietenia dintre triunghiul dreptunghic și cerc.

Suma cuburilor este pătratul sumei lui Gauss

Știți că suma lui Gauss ne spune, de exemplu, că $$1+2+3+...+7=\frac{7\cdot 8}{2}.$$

Așadar, suma primelor n numere naturale este semiprodusul dintre ultimul număr și succesorul său, fapt care se poate exprima prin formula $$1+2+3+\dots n={\color{blue}{\frac{n\cdot(n+1)}{2}}}.$$

Apoi, suma pătratelor se poate exprima printr-o formulă asemănătoare, la care se mai înmulțește o fracție simplă:

$$1^2+2^2+3^2+\dots n^2={\color{blue}{\frac{n\cdot(n+1)}{2}}}\cdot\frac{2n+1}{3}.$$

Dar cea mai interesantă dintre toate este suma cuburilor, care se scrie drept:

$$1^3+2^3+3^3+\dots n^3=(1+2+3+\dots n)^2=\left[{\color{blue}{\frac{n\cdot(n+1)}{2}}}\right]^2!$$

Vă dați seama ce interesantă este această relație? Adică ea ne spune, de exemplu, că: 

$$1^3+2^3+3^3+4^3=(1+2+3+4)^2!$$

Minunată-i Matematica asta!

Cercul și poligoanele regulate

Ca și oricare dintre triunghiuri, cel echilateral are două cercuri prietene, unul circumscris, care trece prin toate vârfurile sale și unul înscris care atinge toate laturile sale. Doar că, pentru triunghiul echilateral, datorită simetriei perfecte a acestuia, centrele celor două cercuri coincid cu centrul de greutate și cu ortocentrul triunghiului. Această coincidență plăcută simplifică legătura dintre lungimea laturii triunghiului echilateral și razele celor două cercuri.

În geogebra am realizat o fișă în care puteți găsi formulele aferente legăturii dintre poligoanele regulate aprofundate în gimnaziu, adică triunghiul echilateral, pătratul și hexagonul regulat.

Vedeți mai jos imaginile corespunzătoare acestor poligoane:

Vă doresc să puteți asimila cât mai multe dintre aceste minunate formule, între care există o legătură profundă.

Inegalitatea mediilor: media aritmetică este mai mare decât media geometrică

Folosindu-ne de cea mai importantă inegalitate din gimnaziu, despre care am discutat în articolul precedent, putem obține o nouă inegalitate importantă, valabilă pentru medii.

Mai exact, dacă pornim de la două numere reale pozitive $0\leq a\leq b$, putem calcula media lor aritmetică dată de $$M_a(a,b)=\frac{a+b}{2}$$ și media lor geometrică $$M_g=\sqrt{a\cdot b}.$$

De exemplu, dacă numerele sunt $a=4$ și $b=9$, atunci media lor aritmetică este $$M_a=\frac{4+9}{2}=\frac{13}{2}=6,5$$ și $$M_g=\sqrt{4\cdot 9}=\sqrt{36}=6.$$

Observați deja că $6,5>6$ și astfel media aritmetică a celor două numere alese este mai mare decât media lor geometrică. 

Această inegalitate este una generală, în sensul că media aritmetică a două (sau mai multor) numere reale pozitive este întotdeauna mai mare sau cel puțin egală cu media lor geometrică. Deci, întotdeauna avem $$\color{red}{\frac{a+b}{2}\geq\sqrt{a\cdot b}}.$$

Căci, pornind de la cea mai importantă inegalitate din gimnaziu, care ne spune că orice număr real ridicat la puterea a doua este mai mare decât zero sau cel puțin egal cu zero, rezultă că acest lucru este valabil și pentru diferența a două numere reale pozitive, oricare ar fi ele $(x-y)^2$, adică avem $$(x-y)^2\geq 0.$$ 

Mai departe, ridicând la puterea a doua paranteza prin înmulțirea parantezei cu ea însăși sau prin utilizarea formulei de calcul prescurtat, vom avea că $$(x-y)^2=(x-y)\cdot(x-y)=x^2-xy-yx+y^2=x^2-2xy+y^2.$$ Și cum $(x-y)^2\geq 0$, rezultă că $$x^2-2xy+y^2\geq 0,$$ ceea ce mai înseamnă și $$x^2+y^2\geq 2xy$$ (am aruncat în dreapta termenul $2xy$) și mai înseamnă și $$\frac{x^2+y^2}{2}\geq xy$$ (am împărțit inegalitatea precedentă cu 2).

Acum, notând $x^2=a$ și $y^2=b$, cum $a$ și $b$ sunt pozitive, va rezulta că $x=\sqrt{a}$, $y=\sqrt{b}$ și $xy=\sqrt{a}\cdot\sqrt{b}=\sqrt{ab}$, ceea ce ne duce direct la inegalitatea mediilor.

Și există o medie (media pătratică) care este chiar mai mare decât media aritmetică. Pentru numerele concrete alese mai sus avem $$M_p=\sqrt{\frac{4^2+9^2}{2}}=\sqrt{48,5}\approx 6,96.$$

Și există o medie (media armonică) care este mai mică decât media geometrică. Media armonică a lui 4 și 9 este $$M_h=\frac{2}{\frac{1}{4}+\frac{1}{9}}=\frac{2}{0,25+0,(1)}\approx 5,53.$$

Astfel, putem sintetiza inegalitatea mediilor mai frumos: $$\color{red}{b\geq\sqrt{\frac{a^2+b^2}{2}}\geq\frac{a+b}{2}\geq\sqrt{ab}\geq\frac{2}{\frac{1}{a}+\frac{1}{b}}\geq a}.$$

Din această inegalitate celebră mai rezultă că dacă oricare două dintre aceste medii sunt egale, va rezulta că și numerele ale căror medii se calculează sunt egale, concluzie foarte subtilă ce este valorificată în unele probleme mai dificile.

Cea mai importantă inegalitate din gimnaziu!

Elevii de clasa a șasea învață să lucreze cu numere negative, mai mici decât zero. Ca exemplu, primesc temperatura mediului înconjurător sau etajele de la subsolul unor clădiri înalte. 

Li se spune că iarna, atunci când este mai frig decât frigul la care îngheață apele curate, temperatura este negativă, mercurul termometrului fiind foarte înghesuit, ocupând volum mai mic, în timp ce vara temperatura este, de regulă, pozitivă, iar mercurul termometrului este extins mai mult, dilatat mai mult. 

De exemplu, atunci când temperatura este de $-3^o$, este mai frig (nivelul mercurului este mai coborât) decât atunci când temperatura este de $+5^o$, iar diferența de temperatură în acest caz este de $8^o$, adică mercurul urcă 8 etaje ca să ajungă de la etajul $-3$ la etajul 5.

Apoi, după ce au învățat numerele negative, învață să lucreze cu puterile acestora și află că dacă exponentul la care se ridică un număr negativ este par, atunci rezultatul ridicării este un număr pozitiv. De exemplu, $(-3)^2=(-3)\cdot(-3)=+9$.

Din acest moment li se poate povesti despre cea mai importantă inegalitate din gimnaziu și anume despre faptul că $$\color{red}{orice^2\geq 0}.$$

Așadar, orice număr învățat în gimnaziu, ridicat la puterea a doua va da un rezultat pozitiv, indiferent de număr. 

În liceu se învață și alt tip de numere (așa-numitele numere complexe), care ridicate la pătrat ne pot da și un rezultat negativ.

Această inegalitate de care v-am vorbit este cea mai importantă, deoarece din ea rezultă o mulțime de alte inegalități. De exemplu, inegalitatea mediilor se demonstrează ușor cu această inegalitate importantă, ceea ce denotă că inegalitatea mediilor este o consecință frumoasă a celei mai importante inegalități din gimnaziu. 

Așadar, dragii mei, rogu-vă să vă amintiți des despre această minunăție învățată în gimnaziu, căci ea vă va scoate din belele în majoritatea cazurilor când vi se va cere să demonstrați o inegalitate.

Despre un generator automat de teste-fulger, în format pdf

Introducere

Am bucuria să anunț apariția primei versiuni (versiunea beta.5) a unui produs românesc foarte interesant și foarte util pentru o mare categorie de clienți, fie că aceștia sunt elevi, profesori sau părinți. Acest proiect, de mare anvergură, a apărut din dorința de a ajuta cât mai multă lume să înțeleagă fără profesor minunata Matematică, precum și să evalueze cunoștințele dobândite din acest domeniu. El va putea inspira și alți profesori, de la alte materii, să conceapă și ei asemenea baze de date din care calculatorul să genereze aleatoriu o mulțime de teste.

Deocamdată a apărut versiunea corespunzătoare clasei a cincea (motiv pentru care versiunea se numește „beta.5”), urmând ca în lunile și anii care vin, în limita timpului disponibil, să construiesc cu migală și pasiune celelalte baze de date până la clasa a douăsprezecea inclusiv.

Descriere

Testele-fulger sunt concepute pentru a verifica rapid cunoștințele fundamentale ale elevilor și a le confrunta cu rezolvările corecte amplasate în partea a doua a fișierului de test.

Ele caută să evite posibilitatea copierii de la colegi sau de pe internet a răspunsurilor, prin limitarea drastică a timpului de rezolvare, corelat cu limitarea dificultății problemelor.

 

Distractorii sunt concepuți cu multă migală, pe principiul ca elevul care știe să poată alege repede răspunsul corect, iar elevul care nu știe să fie, eventual, indus în eroare de unii distractori.

La cerere, testele pot fi diversificate după mai multe criterii, precum clasa, unitatea de învățare și chiar tipul itemilor. Mai precis, pot fi generate teste de clasa a cincea cu probleme dintr-o singură unitate de învățare sau mai multe. De asemenea, pot fi generate teste ale căror probleme să prezinte distractorii (itemi obiectivi cu alegere multiplă) sau să nu prezinte distractorii (itemi semiobiectivi, de completare). Pot fi generate chiar și teste care combină itemi cu distractori și itemi fără distractori.

Pot fi generate cărți întregi cu sute de astfel de teste de tipul ales inițial de către client.

Fiecare problemă generată automat de către calculator are asociat un punctaj, care împreună cu punctajul din oficiu ar trebui să totalizeze 1000 de puncte în cazul unei rezolvări complete și corecte.

Structură

Testul-fulger are un antet în care poate apărea unitatea de învățământ și numele profesorului, precum și momentul generării testului.

Apoi urmează enunțul problemelor din primul test,

care pot fi probleme fără distractori sau probleme cu distractori, după cum apare în cerința clientului:

unitățile de învățare fiind cele din structura programei pentru clasa a cincea:

iar numărul de teste putând fi, de asemenea, modificat după dorință în interiorul fișierului-sursă LaTeX:

Testul mai conține, așa cum am considerat firesc, rezolvările și explicațiile, care apar pe o pagină nouă ca să poată fi imprimate separat și să nu le vadă la început elevul:

Pentru părinți

Părintele poate imprima unul sau mai multe dintre testele alese, împreună cu rezolvările, iar copilul va primi doar partea cu enunțuri pentru a rezolva problemele, urmând ca după rezolvarea testului, să fie confruntată rezolvarea elevului cu rezolvarea propusă prin test. Asemenea teste pot ajuta părinții nu doar să-și evalueze singuri copiii, ci chiar și să le explice rezolvarea.

Pentru profesori

Testele propuse pot ajuta enorm profesorii pentru a le da elevilor teme sau pentru a-i evalua la clasă. În funcție de nivelul clasei, profesorul poate mări (dubla, tripla) sau micșora timpul propus pentru rezolvarea testului.

Foarte important, antetul și filigranul pot fi modificate la cerere pentru profesori, folosindu-se școala și numele profesorului respectiv.

Versiuni

Versiunea de lansare este „beta.5”, însemnând că este vorba despre versiunea beta aferentă clasei a cincea, care garantează existența unui număr suficient de probleme în baza de date aferente clasei a cincea.

Următoarele versiuni vor rămâne versiuni beta până la atingerea a cel puțin 100 de probleme în fiecare unitate de învățare, caz în care versiunile vor deveni 1.5, 1.6 și așa mai departe. Așadar, primul număr al versiunii va reprezenta numărul de sute de probleme din bazele aferente unităților de învățare, iar numărul al doilea, de după punct, reprezintă clasa la care s-a ajuns cu versiunea respectivă în ordinea crescătoare a lor (începând cu clasa a cincea și terminând cu clasa a douăsprezecea).

Astfel, după versiunea beta.5 va urma versiunea beta.6, apoi beta.7 și tot așa până la apariția versiunii beta.12, după care va apărea versiunea 1.5 (cu peste 100 de probleme la fiecare unitate de învățare din clasa a cincea), apoi 1.6 (cu peste 100 de probleme la fiecare unitate de învățare din clasa a șasea) și așa mai departe.

Prețul

Prețul de pornire al acestor teste este stabilit la 10 bani pe problemă, elevii mei beneficiind de gratuitate în cursul întregului an în care le sunt mentor. Astfel, un test care va conține, de exemplu, 15 probleme va costa 1,5 lei.

Dacă clientul dorește 10 teste cu 15 probleme fiecare, se vor însuma 150 de probleme, prețul total devenind astfel 15 lei. Acest preț, împreună cu descrierea testului vor apărea automat la finalul fiecărui fișier pdf generat.

În foaia de calcul „Lungimea bazelor de date” puteți afla câte probleme am reușit să creez în fiecare dintre bazele de date până în prezent, adică găsiți ceva de genul:

V-M+F=2

Acest domn Euler a fost o minune, un înger pe Pământ. Dânsul ne-a lăsat această relație superbă, $$\color{red}{V-M+F=2}$$ care ne face legătura între numărul de Vârfuri, de Muchii și de Fețe ale unui poliedru.

Puteți reține ușor relația domnului Euler, căci literele care apar sunt în ordine alfabetică descrescătoare și avem un semn minus în mijloc.

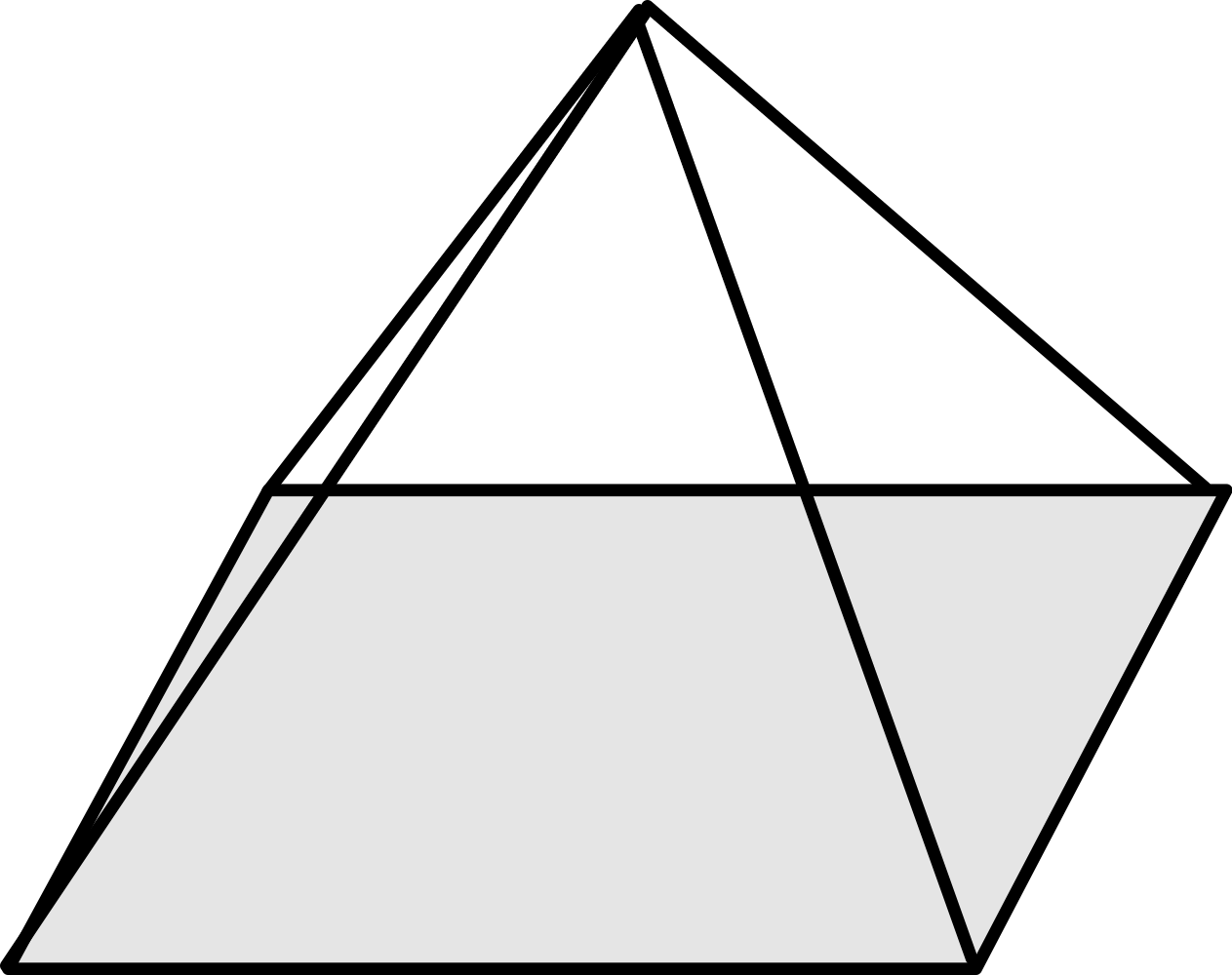
De exemplu, o piramidă patrulateră are 

$V=4+1=5$, cinci vârfuri, $M=2\cdot 4=8$, opt muchii și $F=4+1=5$, cinci fețe. Deci, $V-M+F=5-8+5=\color{red}{2}$.

Mai vedeți și voi alte exemple, poate vă iese tot $\color{red}{2}$.

Sensul unui vector. Orientare. Clasa a IX-a.

Problema 5 din ultimul test ne cere vectorul opus al unui vector. Datorită faptului că un vector este orientat, contează ordinea în care scriem cele două litere care definesc vectorul. Așadar, vectorul XK nu este tot una cu vectorul KX. 

Este adevărat, cei doi vectori XK și KX nu diferă foarte mult între ei, căci au aceeași direcție și același modul. Singurul lucru prin care diferă ei este sensul. Dacă unul dintre ei pleacă „în sus”, celălalt va pleca „în jos”. Dacă unul dintre ei pleacă „spre dreapta”, celălalt va pleca „spre stânga”, iar dacă unul dintre ei va pleca „înainte”, celălalt va pleca „înapoi”. Am pus ghilimele pentru a mă referi la o orientare universală, independentă de suprafața Pământului.

Din acest motiv, cei doi vectori se numesc „opuși”. Așadar, dacă vi se va mai cere vreodată vectorul opus lui XK să știți că vi se cere de fapt vectorul ale cărui litere sunt comutate, adică vectorul KX.

Intersecția mulțimii precedente cu mulțimea numerelor raționale

Dacă în problema precedentă trebuia să intersectăm mulțimea M={-6;-1/5;-sqrt(9);0;sqrt(2);sqrt(3);0,7;8} cu mulțimea numerelor întregi, de data aceasta se cere să o intersectăm cu mulțimea numerelor raționale, notată cu Q. Astfel, elevul care va rezolva această problemă trebuie să cunoască simbolul mulțimii numerelor raționale și mai trebuie să știe ce înseamnă număr rațional sau măcar să poată face distincția dintre numerele raționale și numerele iraționale.


El va ști că tot ce a pus în rezolvarea precedentă (unde trebuia să intersecteze cu Z) va fi bun și în această rezolvare, deoarece orice număr întreg este și rațional. De asemenea, va ști că orice „radical urât”, adică radical cu virgulă va fi număr irațional, deci nu va trebui pus în intersecția cu Q. În mulțimea noastră avem doi radicali urâți, $\sqrt{2}$ și $\sqrt{3}$, deci aceștia nu vor avea ce căuta printre numerele raționale din rezultat.

Drept urmare, intersecția dintre mulțimea M={-6;-1/5;-sqrt(9);0;sqrt(2);sqrt(3);0,7;8} și Q va fi
$$M\cap \mathbb{Q}=\color{red}{\{-6;-1/5;-\sqrt{9};0;0,7;8\}}.$$

Intersecția cu mulțimea numerelor întregi a unei mulțimi care conține tot felul de numere ciudate

În 20 de secunde ar trebui să putem rezolva următoarea problemă simplă de clasa a șaptea, a treia din testul-fulger apărut recent: „Dată fiind mulțimea M={-6;-1/5;-sqrt(9);0;sqrt(2);sqrt(3);0,7;8}, se cere intersecția dintre M și Z. ”

Altfel spus, se cer, de fapt, numerele întregi (căci Z este mulțimea numerelor întregi) din mulțimea M. Căci intersecția a două mulțimi este o nouă mulțime care conține elementele comune din cele două mulțimi, așa cum intersecția a două străzi conține partea comună a celor două străzi.

Ne rămâne atunci să analizăm pe rând fiecare element al mulțimii M ca să putem decide dacă el este număr întreg sau nu este. În cazul în care vom constata că este număr întreg îl vom așeza în noua mulțime, iar în cazul în care nu este număr întreg vom sări peste el.

Numerele întregi sunt cele ce pot fi scrise  fără virgulă și fără fracție. Astfel, primul număr $-6$ este întreg, chiar dacă are semnul minus în față (numerele naturale sunt cele fără minus). Următorul număr, adică $-\frac{1}{5}$ nu poate fi scris fără fracție sau fără virgulă, așa că nu este număr întreg. Apoi, $-\sqrt{9}$ este număr întreg, căci este un radical frumos ce poate fi calculat și ne dă $-\sqrt{9}=-3$, așadar este număr întreg, deci îl vom așeza în mulțimea ce ne dă intersecția. Apoi numărul $0$ este număr întreg, căci este și natural și orice număr natural este și întreg (dar nu și reciproc). Radicalii urâți care urmează, $\sqrt{2}$ și $\sqrt{3}$ nu sunt numere întregi, ba chiar nici măcar numere raționale, căci toți radicalii ăștia urâți, care nu se pot calcula exact, sunt numere iraționale. Ne mai rămâne atunci să analizăm numerele $0,7$ și $8$, dintre care, desigur, doar numărul $8$ este număr întreg, așa cum ne trebuie nouă în rezultat.

Atunci, punând împreună concluziile precedente, înțelegeți mai bine de ce obținem că noua mulțime de la răspuns va fi formată din elementele: $$\color{red}{-6,\,-\sqrt{9},\,0,\,8}.$$

În triunghiul SUV unghiul U este dublul lui V, iar S are 60 de grade. Câte grade are U?

Acesta este enunțul celei de-a doua probleme din politestul pe care îl rezolvăm acum.

Pentru a rezolva problema pornim de la faptul că suma (măsurilor) unghiurilor unui triunghi este 180 de grade, oricât de urât ar fi triunghiul respectiv.  Până aici a fost geometrie, iar de aici încolo va fi algebră. Deci, avem de rezolvat o ecuație. 

Dacă notăm măsura unghiului V cu x, atunci ecuația noastră este $$2x+x+60=180.$$

Așadar, $3x=180-60=120$. De aici rezultă că unghiul V are măsura $x=40$, deci unghiul U, fiind dublul lui V, va avea valoarea $$U=2x=2\cdot 40=\color{red}{80}.$$

Fracție ireductibilă cu numitorul 12

Începem o nouă serie articole în care vom rezolva politestul-fulger de clasa a douăsprezecea apărut în 1 octombrie.

Astăzi, prima problemă ne cere să dăm un exemplu de fracție ireductibilă cu numitorul 12. Elevul de clasa a cincea (și, implicit, cel de clasa a douăsprezecea) trebuie să știe că o fracție este ireductibilă dacă nu se mai poate simplifica. Mai departe, aceasta înseamnă că numărătorul și numitorul sunt relativ prime, adică au cel mai mare divizor comun egal cu unitatea.

Numerele relativ prime nu trebuie să fie neapărat prime. Noțiunea de „relativ” se referă la o comparație între cele două numere, adică unul trebuie să fie prim față de celălalt. De exemplu, numerele 15 și 8, deși nu sunt prime, totuși sunt relativ prime pentru că nu există niciun număr cu care să se poată împărți exact amândouă (cu excepția lui 1, desigur, care este irelevant căci nu modifică nimic).

Așadar, ca să putem crea o fracție ireductibilă cu numitorul 12 este necesar să găsim un număr relativ prim cu 12 pe care să-l așezăm la numărătorul fracției. Desigur că orice număr prim va fi relativ prim cu orice alt număr care nu-l va avea ca divizor pe acel număr prim. Aceasta înseamnă că, de exemplu, orice număr prim mai mare decât 12 ar putea rezolva problema noastră. Mai exact, oricare dintre fracțiile: 

$$\color{red}{\frac{13}{12}},\,\frac{17}{12},\,\frac{19}{12},\,\frac{23}{12},\,\frac{29}{12},\,\dots$$ 

va fi o fracție care duce la rezolvarea problemei.

Da, bineînțeles, cum spunea, nu doar numerele prime mai mari decât 12 pentru numărător sunt soluția. Alte exemple, fără numere prime, pot fi:

$$\frac{25}{12},\,\frac{49}{12},\,\frac{121}{12},\,\frac{125}{12},\,\dots$$

Evident că elevul din clasele terminale ale liceului ar fi bine să cunoască aceste detalii, pentru a putea rezolva problemele mult mai complicate apărute de-a lungul anilor.

Ce valoare are produsul scalar dacă vectorii sunt perpendiculari?

Textul

Ultima problemă din politestul curent

spune „Ce valoare are produsul scalar dacă vectorii sunt perpendiculari?”

În cinci secunde, elevul știe că doi vectori perpendiculari are produsul scalar egal cu zero, deoarece unghiul dintre vectorii perpendiculari fiind un unghi drept, cosinusul acestuia este zero.

În general, produsul scalar dintre doi vectori este un număr dat de un produs de trei factori, doi dintre factori fiind modulele vectorilor respectivi, iar al treilea factor fiind cosinusul unghiului dintre cei doi vectori. Adică:

$$|\vec u|\cdot|\vec v|=uv\cos(\vec u;\vec v).$$

Și cum $$\cos 90^o=0,$$ rezultă ceea ce se constată și la răspunsul din politest.

Care este valoarea extremă a funcției de gradul al doilea $f(x)=-2x^2+6x+5$?

În politestul de clasa a noua pe care îl discutăm acum

găsim problema:

„Fie funcția de gradul al doilea, definită pe R cu valori în R, dată prin $f(x)=-2x^2+6x+5$. Care este valoarea ei extremă?”

Se poate rezolva în 20 de secunde această problemă? Cum dumnezeu? Păi, elevul care știe că valoarea extremă a funcției de gradul al doilea este tocmai ordonata vârfului parabolei va calcula repede pe $\Delta$ și va face raportul necesar. 

Cum vârful parabolei are coordonatele: $$V\left(-\frac{b}{2a};-\frac{\Delta}{4a}\right)$$ și cum ordonata acestui vârf este $$-\frac{\Delta}{4a},$$

rezultă că vom calcula pe $\Delta=36+40=76$ și raportul $$-\frac{\Delta}{4a}=-\frac{76}{-8}=\color{red}{\frac{19}{2}}.$$

Aceasta este valoarea extremă (maximă) a funcției date. Valoarea minimă nu există, căci pentru $a<0$ (coeficientul lui $x^2$ este negativ) parabola are vârful în sus, iar în acest caz cea mai mică valoare posibilă a funcției ar fi $-\infty$, care nu aparține mulțimii numerelor reale (ci numai lui $\mathbb{\bar{R}}$).

Care interval este soluția inecuației $2x-1>7$?

A șaptea problemă din politestul recent de clasa a noua ne cere să găsim soluția unei inecuații. Inecuația nu este complicată și tocmai de aceea primim 20 de secunde pentru rezolvarea ei.

Așadar, să începem. Dacă inecuația este $$2x-1>7,$$ noi o vom transforma în așa fel încât să scăpăm de numerele din jurul lui $x$. Astfel, din $2x-1>7$ putem obține $2x>7+1$, căci l-am aruncat pe $-1$ de lângă $x$ în partea cealaltă a semnului de inegalitate. Și observați că am început cu $-1$, nu cu $2$ deoarece procedăm ca și în cazul „mersului invers” când începem tocmai invers, cu operațiile care se fac ultimele (în acest caz am început cu scăderea și am transformat-o în adunare).

Acum am obținut inecuația echivalentă $$2x>8.$$ Următorul pas este să scăpăm și de $2$ care este înmulțit cu $x$. Pentru aceasta, desigur, vom împărți inecuația cu $2$. Cum $2$ este pozitiv, nu se va schimba semnul inegalității (dacă era negativ, s-ar fi schimbat). Obținem acum $$x>\frac{8}{2},$$ adică $$x>4.$$

Această ultimă formă a inecuației în care am reușit să-l eliberăm pe $x$ de numerele din jurul său este forma finală din care vom putea extrage intervalul cerut. Inecuația ne spune că ne trebuie toate numerele mai mari decât $4$. Toate acele numere sunt soluții ale inecuației date. Și cum exprimăm toate aceste numere ca un interval? Cum putem să ne referim la „toate numerele mai mari decât $4$”? Iată cum: $$\color{red}{(4;+\infty)}.$$

Acest interval este soluția inecuației date.

Ați găsit explicații mai detaliate undeva? Ce mă bucur că pot să vă ajut!

Care sunt elementele mulțimii A={x aparține lui Z | 3/x aparține lui Z}?

A șasea problemă din politestul-fulger pe care îl rezolvăm în această serie de articole ne cere mulțimea elementelor care satisfac o anumită proprietate. Elevul trebuie să înțeleagă cerința și să fie atent la mulțimile care apar în cerință. În cazul problemei noastre în cerință apare mulțimea numerelor întregi, adică a celor ce pot fi scrise simplu fără virgulă (dar care pot fi negative).

Așadar, care sunt elementele mulțimii A={x aparține lui Z | 3/x aparține lui Z}? 

Înainte de toate trebuie să ne uităm la fracția $\frac{3}{x}$ și să studiem ce ar trebui să fie numitorul pentru ca această fracție să fie număr întreg. Desigur, numitorul trebuie să fie un divizor al lui trei. Iar acești divizori ai lui trei pot fi și negativi, deoarece mulțimea Z conține și numere negative. Dacă ar fi fost vorba de N, atunci trebuia să avem grijă să ne limităm doar la divizorii pozitivi, dar mulțimea Z ne permite și numerele negative.

Cum divizorii întregi ai lui $3$ sunt $-3$, $-1$, $1$ și $3$ și cum numitorul nu mai conține altceva decât tocmai necunoscuta $x$, rezultă că răspunsul la problema noastră va fi simplu: $$\color{red}{-3,\,-1,\,1,\,3}.$$

Radical din 8 plus radical din 2 este radical din 18. Interesant, nu-i așa!?

Textul

Problema 5 din politest ne cere un lucru simplu: să adunăm $\sqrt{8}$ cu $\sqrt{2}$.

Sunt elevi care cred că rezultatul ar fi $\sqrt{8+2}$. Alții cred că adunarea nu se poate face, deoarece radicalii nu sunt de același fel.

Dar, de fapt, calculul se poate face ușor după ce ne ocupăm întâi de $\sqrt{8}$ pe care îl transformăm în $2\sqrt{2}$. Astfel, avem:

$$\sqrt{8}+\sqrt{2}=2\sqrt{2}+\sqrt{2}=\color{red}{3\sqrt{2}=\sqrt{18}}.$$

Mai exact, radicalii de același fel se adună ușor, așa cum adunăm merele sau perele. Astfel, doi radicali din 2, adunat cu încă un radical din 2 ne vor da trei radicali din 2, așa cum două mere plus un măr fac trei mere.

Mai rămâne să înțelegem de ce $\sqrt{2}$ poate fi asimilat cu $2\sqrt{2}$. O metodă ar fi descompunerea numărului 8 în factori primi, care ne va da că $8=2^3$. Cum doar doi de 2 se pot împerechea, celălalt 2 rămâne sub radical.

Cealaltă metodă este să observăm că numărul $8$ nu este liber de pătrate, căci în el se ascunde pătratul perfect $4$. Atunci $$\sqrt{8}=\sqrt{4\cdot 2}=\sqrt{4}\cdot\sqrt{2}=2\sqrt{2}.$$

Și consider că astfel v-am arătat detaliile rezolvării acestei probleme frumoase.

Problemă de a șaptea cu paralelogramul ABEL

O altă problemă din testul precedent spune că „În paralelogramul ABEL unghiul E are 70 de grade. Câte grade are unghiul A?".

Se poate rezolva problema în zece secunde, așa cum spune politestul-fulger? Bineînțeles. Oare trebuie desenat paralelogramul? Nicidecum. Este suficient să știm că ordinea literelor ne spune că unghiul A este opus unghiului E și că unghiurile opuse într-un paralelogram sunt egale. Gata.

Nu-i așa că aceste teste scot la iveală rapid și sigur cunoștințele fundamentale ale elevului? Nu-i așa că asemenea teste pot fi folosite chiar și cu cărțile în față? Cine știe nu mai are nevoie să caute și se încadrează în timp, iar cine are nevoie să caute nu știe și nu se încadrează în timp.

Cercul circumscris și mediatoarele

A doua problemă din politestul de clasa a IX-a apărut în 29 august este acum de clasa a șasea. Observați că politestele de clasa a IX-a au o problemă de a cincea și câte două problemele din clasele următoare.

Această primă problemă de clasa a șasea ne spune: în triunghiul VOR centrul cercului circumscris se află la 12 cm de punctul V. Se cere distanța de la punctul de intersecție a mediatoarelor triunghiului VOR la punctul O.

Problema este extrem de simplă și ar putea fi rezolvată în mai puțin de un minut de către elevul care știe că punctul de intersecție a mediatoarelor triunghiului este tocmai centrul cercului circumscris triunghiului dat. Dar elevul care nu cunoaște această proprietate este pierdut. Tot pierdut este și elevul care nu înțelege textul și, implicit, nu înțelege cerința problemei.

Elevul care știe că centrul cercului circumscris este la intersecția mediatoarelor știe că acest centru este la distanțe egale de vârfurile triunghiului, aceste distanțe fiind razele cercului circumscris, deci știe că răspunsul va fi tot 12 cm.

Desigur, elevul „pierdut” ar trebui să poată redescoperi proprietatea conform căreia centrul cercului circumscris este la intersecția mediatoarelor. Adică, ar trebui să știe ce este o mediatoare și să știe că orice punct de pe mediatoare se află la distanțe egale de capetele segmentului mediat. Atunci ar deduce că cel puțin două dintre mediatoare se intersectează într-un punct aflat la distanță egală de capetele ambelor segmente mediate, deci la distanță egală de vârfurile triunghiului.

Prima problemă din politestul-fulger de clasa a IX-a, generat în 29 august

În cele ce urmează ne vom ocupa de un politest-fulger din imaginea de mai jos, în care vedeți o listă cu 9 probleme, prima de clasa a cincea și apoi câte două din fiecare clasă până într-a noua inclusiv. Baza de itemi acoperită are 938 de elemente momentan, iar politestul apărut ar trebui să poată fi rezolvat în 270 de secunde.

Prima problemă, de clasa a cincea, ne spune că „Segmentul LH are lungimea de 8 cm, segmentul HV are lungimea de 50 mm, iar punctele H, V și L sunt coliniare în această ordine. Ce lungime are segmentul VL?”.

Dacă punctele H, V și L sunt coliniare în această ordine, atunci suma segmentelor mici trebuie să ne dea exact segmentul mare. Mai concret, 

$$HV+VL=HL.$$

Așadar, elevul de clasa a cincea care întâlnește această problemă trebuie să înțeleagă enunțul, să își amintească ce înseamnă coliniaritatea celor trei puncte și ce consecință metrică are această coliniaritate. Desigur că în 60 de secunde se poate realiza aceasta.

Urmează atunci o simplă înlocuire, în care ținem seama că segmentul $HL$ are aceeași lungime cu segmentul $LH$, astfel că relația precedentă devine:
$$HV+VL=HL\Longrightarrow 50\, \text{mm}+VL=8\,\text{cm}.$$

Următoarea etapă de rezolvare a problemei este transformarea unităților de măsură pentru a putea omogeniza relația, formă în care vom putea calcula lungimea lui VL. Căci, un elev superficial care s-ar grăbi să facă asemenea calcule fără să țină seama de faptul că unitățile de măsură sunt diferite, ar ajunge la un rezultat aberant și anume ar fi nevoit să facă scăderea $8-50$ care l-ar duce la un rezultat număr negativ.

Așadar, contează mult unitatea de măsură. O valoare numerică singură, fără unitatea de măsură asociată nu ne dă nicio informație despre lungimea segmentelor. Numai ansamblul celor două ne poate da precizia de care este nevoie.

Atunci trebuie să transformăm centimetri în milimetri sau milimetri în centimetri. Alegem ultima variantă. Cum 50 de milimetri înseamnă 5 centimetri, relația noastră devine acum omogenă:

$$50\, \text{mm}+VL=8\,\text{cm}\Longrightarrow 5\, \text{cm}+VL=8\,\text{cm}.$$

Din această ultimă relație rezultă că 
$$VL=8\,\text{cm}-5\,\text{cm}=\color{red}{3\,\text{cm}}.$$

Ultima problemă din testul generat automat în 5 august

A noua problemă, deci ultima, ne cere să găsim cel mai mic număr natural din intervalul (-7; 4]. Cu puțină atenție, elevul nu va confunda cerința. Căci, în timp ce un elev neatent ar putea crede că răspunsul este $-6$, elevul vigilent va observa că se cere numărul care trebuie să fie natural, nu întreg. 

Și cum numerele naturale nu sunt negative, cel mai mic număr natural posibil este numărul $0$. Și cum acest număr se regăsește în intervalul dat, răspunsul final va fi, desigur, $\color{red}{0}$.

Problema 8 din testul precedent, geometrie cu teorema medianei principale și a unghiului de 30

A opta problemă din test, de geometrie, ne spune că avem cateta mică de 14 cm și se cere distanța de la vârful unghiului mic la suportul medianei principale. Oare putem rezolva problema în 45 de secunde?

Elevul harnic va schița repede un desen de genul:

Acest desen este justificat de două teoreme importante pe care le-a învățat deja elevul isteț de clasa a șaptea: teorema unghiului de 30 de grade (care poate fi înlocuită și de funcțiile trigonometrice) și teorema medianei principale (cea corespunzătoare ipotenuzei).

Mai precis, elevul care știe ce este mediana corespunzătoare ipotenuzei va pregăti dreapta roșie, căci aceasta conține mediana care pornește din vârful unghiului de 90 de grade și se duce pe mijlocul M al ipotenuzei.

De asemenea, dacă știe ce înseamnă distanță de la un punct la o dreaptă, va duce frumos o perpendiculară (albastră) pe dreapta roșie din vârful unghiului mic, de 30 de grade, așa cum cere problema. 

Cu desenul făcut își va aminti că triunghiul dreptunghic special (Timaios) care are un unghi de 30 de grade este un triunghi cu proprietăți minunate (iar pentru studiul acestui triunghi are un echer cu un unghi de 30 de grade). Mai exact, își va aminti teorema unghiului de 30 de grade care spune că într-un asemenea triunghi dreptunghic special (ce cu unghiul de 30 de grade) ipotenuza este dublul catetei mici. 

Cunoscând ipotenuza și cateta mică, el poate determina cu teorema lui Pitagora lungimea catetei mari. Sau, dacă este și mai isteț, el poate reține că lungimea catetei mari în triunghiul acesta minunat este ca și a celei mici, doar că îi mai lipim un radical din trei. Sau, dacă îi plac funcțiile trigonometrice, va putea afla direct cateta mare din cateta mică cu ajutorul funcției tangentă de 30 de grade care este raportul dintre cateta opusă unghiului de 30 de grade (cea mică în cazul nostru) și cateta alăturată (cea mare).

Odată ce a găsit lungimea catetei mari, elevul nostru va trebui să-și amintească teorema medianei principale care îi va spune că în orice triunghi dreptunghic (nu doar în cel cu un unghi de 30 de grade) mediana corespunzătoare ipotenuzei este și ea jumătate din ipotenuză, ceea ce înseamnă că triunghiul AMB este isoscel, deci și unghiul BAD este de 30 de grade, deci și în triunghiul BAD poate folosi teorema unghiului de 30 de grade, deci cateta mică din acest triunghi, adică BD va fi jumătate din ipotenuza triunghiului BAD, care ipotenuză este acum AB, adică fosta catetă mare din triunghiulABC, a cărei lungime a găsit că este $14\sqrt{3}$. 

Și cum jumătate din $14\sqrt{3}$ este $\color{red}{7\sqrt{3}}$, elevul care știe dinainte, fără să clipească, toate aceste lucruri, poate finaliza rezolvarea într-un timp rezonabil, din câteva priviri ale desenului făcut corect.

Problema 6 din testul-fulger: calculează $\frac{21+\sqrt{98}}{3+\sqrt{2}}$

Pentru a face calculul cerut de problema 6 în 60 de secunde

$$\frac{21+\sqrt{98}}{3+\sqrt{2}}$$

va trebui să aducem la o formă mai simplă expresia, așa cum spuneam la problema 4 deja rezolvată. Dar, de data aceasta, numitorul acestei fracții urâte este oarecum mai complicat, căci are o adunare și ar însemna că raționalizarea numitorului acestei fracții ar fi ceva mai laborioasă decât a fost la problema 4.

Rezolvarea cu factorul comun

Mai bine, dacă aruncăm o privire la numărătorul fracției (partea de sus), constatăm că acolo se află radicalul $\sqrt{98}$ pe care elevul cu experiență știe că trebuie să-l modifice puțin, adică „să scoată factorul de sub radical”, căci numărul 98 nu este „liber de pătrate”, în el ascunzându-se pătratul perfect $49$. Așadar, din $\sqrt{98}$ putem să facem $$\sqrt{98}=\sqrt{49\cdot 2}=\sqrt{49}\cdot\sqrt{2}=7\sqrt{2}.$$

Cu această observație, fracția noastră devine acum 
$$\frac{21+\sqrt{98}}{3+\sqrt{2}}=\frac{21+7\sqrt{2}}{3+\sqrt{2}}.$$

Acum numărătorul are o poveste fascinantă, care ne va permite să rezolvăm mai repede problema decât am fi rezolvat-o dacă porneam pe drumul raționalizării. Mai exact, expresia $21+7\sqrt{2}$ ne permite să dăm factorul comun pe $7$, deoarece $21=7\cdot 3$. Atunci calculul nostru devine mult mai interesant:

$$\frac{21+\sqrt{98}}{3+\sqrt{2}}=\frac{21+7\sqrt{2}}{3+\sqrt{2}}=\frac{7(3+\sqrt{2})}{3+\sqrt{2}}.$$

Sunt convins că acum ați observat deja magia calculului care urmează: putem simplifica cu $\color{blue}{3+\sqrt{2}}$! Yuuuuppppiiii! Ce simplu a fooost! Așadar, simplificând obținem 

$$\frac{21+\sqrt{98}}{3+\sqrt{2}}=\frac{21+7\sqrt{2}}{3+\sqrt{2}}=\frac{7(\color{blue}{3+\sqrt{2}})}{\color{blue}{3+\sqrt{2}}}=\frac{7}{1}=\color{red}{7}.$$

Rezolvarea cu raționalizarea

Desigur, dacă am fi urmat drumul raționalizării înainte să observăm că se naște factorul comun ce ne va permite simplificarea, am fi ajuns la aceeași valoare, căci Matematica este coerentă, doar că ne-ar fi purtat pe căi mai întortocheate. Iată cam ce însemna raționalizarea numitorului, deci amplificarea cu conjugata.

Știm că atunci când avem o sumă (sau diferență) cu radicali la numitor, putem amplifica fracția cu așa-numita „expresie conjugată”, adică exact aceeași expresie care se regăsește deja la numitor, doar că cu semnul schimbat (dacă este sumă, amplificăm cu diferența, iar dacă e diferență amplificăm cu suma).

Atunci, făcând amplificarea și muncind cu răbdare pentru a desface apoi parantezele prin înmulțirea termenilor corespunzători, avem

$$\frac{21+\sqrt{98}}{3+\sqrt{2}}=\frac{(3-\sqrt{2})(21+\sqrt{98})}{(3-\sqrt{2})(3+\sqrt{2})}=$$

$$=\frac{63+3\sqrt{98}-21\sqrt{2}-\sqrt{2}\sqrt{98}}{9-2}.$$

Observați că pentru numitor am folosit formula de calcul prescurtat care spune că $$\color{red}{(a-b)(a+b)=a^2-b^2},$$ adică $(3-\sqrt{2})(3+\sqrt{2})=3^2-(\sqrt{2})^2=9-2$.

Apoi, ocupându-ne de numărător și observând că $3\sqrt{98}=3\cdot 7\sqrt{2}=21\sqrt{2}$, care se va reduce cu $-21\sqrt{2}$ și observând că produsul acela de radicali va da $\sqrt{2}\sqrt{98}=\sqrt{196}=14$, calculul nostru devine atunci 

$$\frac{63+3\sqrt{98}-21\sqrt{2}-\sqrt{2}\sqrt{98}}{9-2}=\frac{63-14}{7}=\frac{49}{7}=\color{red}{7}.$$

O groază de lucru cu raționalizarea asta, dar măcar tot i-am dat de capăt și am ajuns la același rezultat.