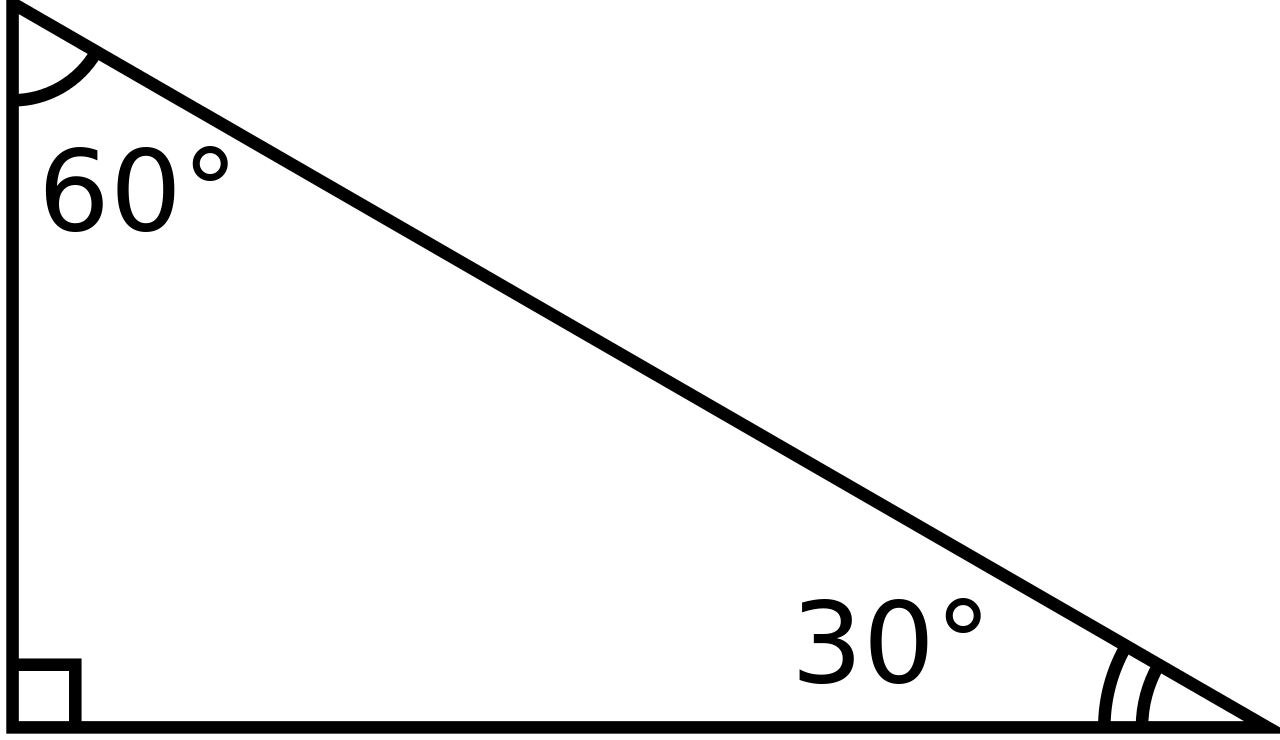
Există în comerț o trusă de instrumente pentru geometrie care, printre o mulțime de alte bunătăți, conține și o piesă extrem de drăguță despre care doresc să vă vorbesc aici și anume „echerul special”. Mai exact, există acolo un echer, care mie îmi este tare drag, ce are un unghi de 30°, un unghi de 60° și un unghi drept, adică de 90°. Acest echer, mai bine zis, acest triunghi dreptunghic, are o importanță supremă în geometrie, deoarece apare foarte, foarte des în problemele pe care le veți întâlni vreodată.
El ne amintește de o proprietate fundamentală în geometrie pe care o are triunghiul acesta dreptunghic cu un unghi de 30°: cateta mică este jumătate din ipotenuză. În aceste șase cuvinte magice este cuprinsă o proprietate geometrică pe care o veți întâlni în sute de probleme de acum încolo. Ea ne spune că în acest triunghi dreptunghic special, cateta mică (adică latura aceea care formează unghiul drept și care este departe de unghiul de 30°), este tocmai jumătate din ipotenuză, deci este tocmai jumătate din cea mai lungă latură a triunghiului dreptunghic special.
Concret, dacă veți avea curiozitatea să măsurați cu liniarul lungimea ipotenuzei echerului special, după care să măsurați lungimea catetei mici a acestui echer, veți constata că, așa ca printr-o minune, cateta mică este jumătate din ipotenuză. Așadar, mai putem spune și că ipotenuza este de două ori mai mare decât cateta mică.
Bineînțeles, această proprietate este valabilă pentru orice triunghi dreptunghic special (deci, triunghi cu unghiurile de 30°, 60°, 90°) și ea este echivalentă cu faptul că sinus de 30° este unu supra doi ($\frac 1 2$), sinusul unui unghi fiind, prin definiție, cateta opusă acelui unghi supra ipotenuză.
El ne amintește de o proprietate fundamentală în geometrie pe care o are triunghiul acesta dreptunghic cu un unghi de 30°: cateta mică este jumătate din ipotenuză. În aceste șase cuvinte magice este cuprinsă o proprietate geometrică pe care o veți întâlni în sute de probleme de acum încolo. Ea ne spune că în acest triunghi dreptunghic special, cateta mică (adică latura aceea care formează unghiul drept și care este departe de unghiul de 30°), este tocmai jumătate din ipotenuză, deci este tocmai jumătate din cea mai lungă latură a triunghiului dreptunghic special.
Concret, dacă veți avea curiozitatea să măsurați cu liniarul lungimea ipotenuzei echerului special, după care să măsurați lungimea catetei mici a acestui echer, veți constata că, așa ca printr-o minune, cateta mică este jumătate din ipotenuză. Așadar, mai putem spune și că ipotenuza este de două ori mai mare decât cateta mică.
Bineînțeles, această proprietate este valabilă pentru orice triunghi dreptunghic special (deci, triunghi cu unghiurile de 30°, 60°, 90°) și ea este echivalentă cu faptul că sinus de 30° este unu supra doi ($\frac 1 2$), sinusul unui unghi fiind, prin definiție, cateta opusă acelui unghi supra ipotenuză.


Niciun comentariu:
Trimiteți un comentariu
Exprimați-vă părerea despre articol sau cereți lămuriri suplimentare, ca să transmitem cât mai multă informație celor care au nevoie de ea.
Comentariul va apărea după un anumit interval de timp necesar moderării.